| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 6 (Before Exercise 9.1) | Exercise 9.1 | Example 7 to 14 (Before Exercise 9.2) |
| Exercise 9.3 | ||
Chapter 9 Perimeter and Area
Welcome to the solutions guide for Chapter 9, "Perimeter and Area," a crucial chapter in the latest Class 7 NCERT mathematics textbook designated for the academic session 2024-25. This chapter significantly expands upon the foundational concepts of measuring plane figures introduced in Class 6, venturing into new shapes and more complex application scenarios. Mastering the calculation of perimeter (or circumference for circles) and area is fundamental not only for geometry but also for numerous practical applications in science, engineering, design, and everyday life. These solutions provide comprehensive, step-by-step methods to navigate the exercises, ensuring students develop both conceptual understanding and computational proficiency.
While building upon the prior knowledge of perimeter and area for squares ($P=4s, A=s^2$) and rectangles ($P=2(l+b), A=l \times b$), this chapter introduces students to calculating the area of other important quadrilaterals and triangles. A primary focus is on:
- Parallelograms: The solutions clearly explain how to calculate the area using the formula Area = base × height, denoted as $A = b \times h$. Emphasis is placed on correctly identifying the base ($b$) and the corresponding perpendicular height ($h$), distinguishing it from the slant side.
- Triangles: The area calculation is thoroughly demonstrated using the fundamental formula Area = $\frac{1}{2}$ × base × height, or $A = \frac{1}{2} b h$. Again, the solutions highlight the importance of using the perpendicular height relative to the chosen base.
A significant and exciting addition at the Class 7 level is the introduction to Circles. These solutions meticulously explain the key concepts associated with this unique shape:
- The radius ($r$): The distance from the center to any point on the circle.
- The diameter ($d$): The distance across the circle passing through the center ($d=2r$).
- The constant Pi ($\pi$): The ratio of a circle's circumference to its diameter, an irrational number approximately equal to $\frac{22}{7}$ or $3.14$. The solutions will specify which value of $\pi$ to use as per the textbook instructions for specific problems.
- The Circumference ($C$): The 'perimeter' or distance around the circle, calculated using the formulas $C = 2\pi r$ or $C = \pi d$.
- The Area ($A$): The measure of the surface enclosed by the circle, calculated using the formula $A = \pi r^2$.
Beyond these basic shapes, the chapter delves into more complex, practical problems. The solutions provide clear strategies for tackling scenarios such as:
- Calculating the area of paths: This involves finding the area of uniform paths constructed either inside or outside a given shape (often rectangular or circular) by calculating the difference between the areas of the outer and inner boundaries.
- Finding the area of composite figures: These are shapes formed by combining basic geometric figures (rectangles, squares, triangles, semi-circles, etc.). The solutions demonstrate how to break down these complex shapes into simpler components, calculate their individual areas, and then add or subtract them as necessary to find the total area.
Regarding the rationalized syllabus for 2024-25, Chapter 9, "Perimeter and Area," in the Class 7 NCERT textbook maintains its focus on the core formulas and applications for parallelograms, triangles, circles, paths, and basic composite figures. The rationalization mainly involved adjusting the complexity and quantity of exercises, particularly those involving very intricate composite shapes or multi-step conversions, ensuring a strong grasp of fundamental applications without overwhelming students. By utilizing these detailed solutions, students can confidently apply formulas for a wider array of shapes, develop robust problem-solving strategies for practical scenarios, and solidify their understanding of geometric measurements.
Example 1 to 6 (Before Exercise 9.1)
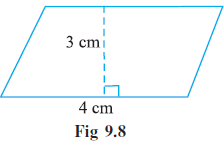
Example 1. One of the sides and the corresponding height of a parallelogram are 4 cm and 3 cm respectively. Find the area of the parallelogram (Fig 9.8).
Answer:
Solution:
Given:
Base of the parallelogram ($b$) = 4 cm.
Corresponding height of the parallelogram ($h$) = 3 cm.
To Find:
The area of the parallelogram.
Solution:
The area of a parallelogram is given by the formula:
$ \text{Area} = \text{base} \times \text{height} $
Substituting the given values into the formula:
$ \text{Area} = b \times h $
$ \text{Area} = 4 \text{ cm} \times 3 \text{ cm} $
$ \text{Area} = 12 \text{ cm}^2 $
The unit of area is square centimetres, denoted as $\text{cm}^2$.
Conclusion: The area of the parallelogram is $12 \text{ cm}^2$.
Example 2. Find the height ‘x’ if the area of the parallelogram is 24 cm2 and the base is 4 cm.
Answer:
Solution:
Given:
Area of the parallelogram = $24 \text{ cm}^2$.
Base of the parallelogram ($b$) = 4 cm.
Height of the parallelogram ($h$) = x cm.
To Find:
The value of the height 'x'.
Solution:
The formula for the area of a parallelogram is:
$ \text{Area} = \text{base} \times \text{height} $
$ \text{Area} = b \times h $
Substitute the given values into the formula:
$24 \text{ cm}^2 = 4 \text{ cm} \times x$
To find the value of x, we can rearrange the equation:
$x = \frac{24 \text{ cm}^2}{4 \text{ cm}}$
$x = 6$
The unit for height is cm.
So, $x = 6 \text{ cm}$.
Conclusion: The height of the parallelogram is 6 cm. Thus, $x = 6$.
Example 3. The two sides of the parallelogram ABCD are 6 cm and 4 cm. The height corresponding to the base CD is 3 cm (Fig 9.10). Find the
(i) area of the parallelogram.
(ii) the height corresponding to the base AD.

Answer:
Solution:
Given:
Parallelogram ABCD.
Length of side CD = 6 cm.
Length of side AD = 4 cm.
Height corresponding to base CD = 3 cm.
To Find:
(i) Area of the parallelogram ABCD.
(ii) Height corresponding to the base AD.
Solution:
(i) Area of the parallelogram:
The area of a parallelogram is given by the formula:
$ \text{Area} = \text{base} \times \text{corresponding height} $
We are given the base CD and its corresponding height.
Base (CD) = 6 cm.
Height corresponding to CD = 3 cm.
Substitute the values into the formula:
$ \text{Area} = \text{CD} \times (\text{height corresponding to CD}) $
$ \text{Area} = 6 \text{ cm} \times 3 \text{ cm} $
$ \text{Area} = 18 \text{ cm}^2 $
The area of the parallelogram is $18 \text{ cm}^2$.
(ii) The height corresponding to the base AD:
We know the area of the parallelogram from part (i) is $18 \text{ cm}^2$.
We are given the base AD = 4 cm.
Let the height corresponding to the base AD be $h_{AD}$.
Using the area formula with base AD:
$ \text{Area} = \text{AD} \times h_{AD} $
Substitute the known values:
$18 \text{ cm}^2 = 4 \text{ cm} \times h_{AD}$
To find $h_{AD}$, rearrange the equation:
$h_{AD} = \frac{18 \text{ cm}^2}{4 \text{ cm}}$
$h_{AD} = \frac{18}{4} \text{ cm}$
Simplify the fraction:
$h_{AD} = \frac{\cancel{18}^{9}}{\cancel{4}_{2}} \text{ cm} = \frac{9}{2} \text{ cm}$.
This can also be written as a decimal: $h_{AD} = 4.5 \text{ cm}$.
The height corresponding to the base AD is $\frac{9}{2}$ cm or 4.5 cm.
Conclusion:
(i) The area of the parallelogram is $18 \text{ cm}^2$.
(ii) The height corresponding to the base AD is $\frac{9}{2}$ cm (or 4.5 cm).
Example 4. Find the area of the following triangles (Fig 9.11).
Fig 9.11

Answer:
Solution:
The area of a triangle is given by the formula:
$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $
$ \text{Area} = \frac{1}{2} \times b \times h $
In the given figure (Fig 9.11), there are two triangles shown.
(i) For the first triangle (on the left):
From the figure, the base ($b$) = 4 cm.
The corresponding height ($h$) = 2 cm.
Substitute these values into the area formula:
$ \text{Area}_1 = \frac{1}{2} \times 4 \text{ cm} \times 2 \text{ cm} $
$ \text{Area}_1 = \frac{1}{2} \times 8 \text{ cm}^2 $
$ \text{Area}_1 = 4 \text{ cm}^2 $
The area of the first triangle is $4 \text{ cm}^2$.
(ii) For the second triangle (on the right):
From the figure, the base ($b$) = 3 cm.
The corresponding height ($h$) = 2 cm.
Substitute these values into the area formula:
$ \text{Area}_2 = \frac{1}{2} \times 3 \text{ cm} \times 2 \text{ cm} $
$ \text{Area}_2 = \frac{1}{2} \times 6 \text{ cm}^2 $
$ \text{Area}_2 = 3 \text{ cm}^2 $
The area of the second triangle is $3 \text{ cm}^2$.
Conclusion:
(i) The area of the first triangle is $4 \text{ cm}^2$.
(ii) The area of the second triangle is $3 \text{ cm}^2$.
Example 5. Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm (Fig 9.12).

Answer:
Solution:
Given:
Triangle ABC.
Area of triangle ABC = $36 \text{ cm}^2$.
Height AD corresponding to base BC = 3 cm.
Base BC = ?
To Find:
The length of the base BC.
Solution:
The area of a triangle is given by the formula:
$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $
$ \text{Area} = \frac{1}{2} \times b \times h $
In this case, the base is BC and the corresponding height is AD.
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times \text{BC} \times \text{AD} $
Substitute the given values into the formula:
$36 \text{ cm}^2 = \frac{1}{2} \times \text{BC} \times 3 \text{ cm}$
To find BC, we can rearrange the equation:
$36 = \frac{3}{2} \times \text{BC}$
Multiply both sides by 2:
$36 \times 2 = 3 \times \text{BC}$
$72 = 3 \times \text{BC}$
Divide both sides by 3:
$\text{BC} = \frac{72}{3}$
$\text{BC} = 24$.
The unit for length is cm.
So, BC = 24 cm.
Conclusion: The length of the base BC is 24 cm.
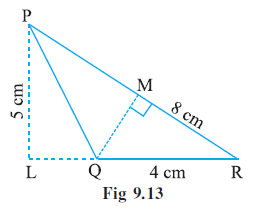
Example 6. In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm (Fig 9.13). Find:
(i) the area of the ∆PQR
(ii) QM
Answer:
Given:
Triangle PQR.
Side PR = 8 cm.
Side QR = 4 cm.
PL is the height corresponding to base QR, PL = 5 cm.
QM is the height corresponding to base PR.
To Find:
(i) The area of $\Delta$PQR.
(ii) The length of QM.
Solution:
(i) The area of $\Delta$PQR:
The area of a triangle is given by the formula:
$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{corresponding height} $
$ \text{Area} = \frac{1}{2} \times b \times h $
We are given the base QR and its corresponding height PL.
Base (QR) = 4 cm.
Corresponding height (PL) = 5 cm.
Substitute the values into the formula:
$ \text{Area of } \Delta \text{PQR} = \frac{1}{2} \times \text{QR} \times \text{PL} $
$ \text{Area of } \Delta \text{PQR} = \frac{1}{2} \times 4 \text{ cm} \times 5 \text{ cm} $
$ \text{Area of } \Delta \text{PQR} = \frac{1}{2} \times 20 \text{ cm}^2 $
$ \text{Area of } \Delta \text{PQR} = 10 \text{ cm}^2 $
The area of the triangle PQR is $10 \text{ cm}^2$.
(ii) QM:
We know the area of $\Delta$PQR from part (i) is $10 \text{ cm}^2$.
We are given the base PR = 8 cm.
QM is the height corresponding to the base PR.
Using the area formula with base PR:
$ \text{Area of } \Delta \text{PQR} = \frac{1}{2} \times \text{PR} \times \text{QM} $
Substitute the known values:
$10 \text{ cm}^2 = \frac{1}{2} \times 8 \text{ cm} \times \text{QM}$
Simplify the equation:
$10 = 4 \times \text{QM}$
To find QM, rearrange the equation:
$\text{QM} = \frac{10}{4} \text{ cm}$.
Simplify the fraction:
$\text{QM} = \frac{\cancel{10}^{5}}{\cancel{4}_{2}} \text{ cm} = \frac{5}{2} \text{ cm}$.
This can also be written as a decimal: QM = 2.5 cm.
The height corresponding to the base PR (QM) is $\frac{5}{2}$ cm or 2.5 cm.
Conclusion:
(i) The area of $\Delta$PQR is $10 \text{ cm}^2$.
(ii) The length of QM is $\frac{5}{2}$ cm (or 2.5 cm).
Exercise 9.1
Question 1. Find the area of each of the following parallelograms:

Answer:
Solution:
The area of a parallelogram is given by the formula:
$ \text{Area} = \text{base} \times \text{corresponding height} $
$ \text{Area} = b \times h $
(a)
From the figure, the base ($b$) = 7 cm.
The corresponding height ($h$) = 4 cm.
Area = $7 \text{ cm} \times 4 \text{ cm}$
Area = $28 \text{ cm}^2$
The area of the parallelogram is $28 \text{ cm}^2$.
(b)
From the figure, the base ($b$) = 5 cm.
The corresponding height ($h$) = 3 cm.
Area = $5 \text{ cm} \times 3 \text{ cm}$
Area = $15 \text{ cm}^2$
The area of the parallelogram is $15 \text{ cm}^2$.
(c)
From the figure, the base ($b$) = 2.5 cm.
The corresponding height ($h$) = 3.5 cm.
Area = $2.5 \text{ cm} \times 3.5 \text{ cm}$
Area = $(2.5 \times 3.5) \text{ cm}^2$
Area = $8.75 \text{ cm}^2$
The area of the parallelogram is $8.75 \text{ cm}^2$.
(d)
From the figure, the base ($b$) = 5 cm.
The corresponding height ($h$) = 4.8 cm.
Area = $5 \text{ cm} \times 4.8 \text{ cm}$
Area = $(5 \times 4.8) \text{ cm}^2$
Area = $24.0 \text{ cm}^2 = 24 \text{ cm}^2$
The area of the parallelogram is $24 \text{ cm}^2$.
(e)
From the figure, the base ($b$) = 2 cm.
The corresponding height ($h$) = 4.4 cm.
Area = $2 \text{ cm} \times 4.4 \text{ cm}$
Area = $(2 \times 4.4) \text{ cm}^2$
Area = $8.8 \text{ cm}^2$
The area of the parallelogram is $8.8 \text{ cm}^2$.
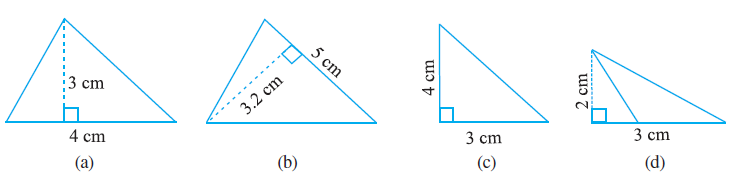
Question 2. Find the area of each of the following triangles:
Answer:
Solution:
The area of a triangle is given by the formula:
$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{corresponding height} $
$ \text{Area} = \frac{1}{2} \times b \times h $
(a)
From the figure, the base ($b$) = 4 cm.
The corresponding height ($h$) = 3 cm.
Area = $\frac{1}{2} \times 4 \text{ cm} \times 3 \text{ cm}$
Area = $\frac{1}{2} \times 12 \text{ cm}^2$
Area = $6 \text{ cm}^2$
The area of the triangle is $6 \text{ cm}^2$.
(b)
From the figure, the base ($b$) = 5 cm.
The corresponding height ($h$) = 3.2 cm.
Area = $\frac{1}{2} \times 5 \text{ cm} \times 3.2 \text{ cm}$
Area = $\frac{1}{2} \times 16 \text{ cm}^2$
Area = $8 \text{ cm}^2$
The area of the triangle is $8 \text{ cm}^2$.
(c)
From the figure, this is a right-angled triangle.
Let the base ($b$) = 3 cm.
The corresponding height ($h$) = 4 cm.
Area = $\frac{1}{2} \times 3 \text{ cm} \times 4 \text{ cm}$
Area = $\frac{1}{2} \times 12 \text{ cm}^2$
Area = $6 \text{ cm}^2$
The area of the triangle is $6 \text{ cm}^2$.
(d)
From the figure, the base ($b$) = 3 cm.
The corresponding height ($h$) = 2 cm (The height is drawn from the vertex to the extended base).
Area = $\frac{1}{2} \times 3 \text{ cm} \times 2 \text{ cm}$
Area = $\frac{1}{2} \times 6 \text{ cm}^2$
Area = $3 \text{ cm}^2$
The area of the triangle is $3 \text{ cm}^2$.
Question 3. Find the missing values:
| S.No. | Base | Height | Area of the Parallelogram |
|---|---|---|---|
| a. | 20 cm | 246 cm2 | |
| b. | 15 cm | 154.5 cm2 | |
| c. | 8.4 cm | 48.72 cm2 | |
| d. | 15.6 cm | 16.38 cm2 |
Answer:
Solution:
The area of a parallelogram is given by the formula:
$ \text{Area} = \text{base} \times \text{height} $
$ A = b \times h $
We can find the missing value by rearranging the formula:
$ h = \frac{A}{b} $
$ b = \frac{A}{h} $
(a)
Given: Base ($b$) = 20 cm, Area ($A$) = 246 cm$^2$.
To find: Height ($h$).
Using the formula $h = \frac{A}{b}$:
$h = \frac{246 \text{ cm}^2}{20 \text{ cm}}$
$h = \frac{246}{20} \text{ cm}$
$h = \frac{123}{10} \text{ cm}$
$h = 12.3 \text{ cm}$
The missing height is 12.3 cm.
(b)
Given: Height ($h$) = 15 cm, Area ($A$) = 154.5 cm$^2$.
To find: Base ($b$).
Using the formula $b = \frac{A}{h}$:
$b = \frac{154.5 \text{ cm}^2}{15 \text{ cm}}$
$b = \frac{154.5}{15} \text{ cm}$
$b = 10.3 \text{ cm}$
The missing base is 10.3 cm.
(c)
Given: Height ($h$) = 8.4 cm, Area ($A$) = 48.72 cm$^2$.
To find: Base ($b$).
Using the formula $b = \frac{A}{h}$:
$b = \frac{48.72 \text{ cm}^2}{8.4 \text{ cm}}$
$b = \frac{48.72}{8.4} \text{ cm}$
$b = 5.8 \text{ cm}$
The missing base is 5.8 cm.
(d)
Given: Base ($b$) = 15.6 cm, Area ($A$) = 16.38 cm$^2$.
To find: Height ($h$).
Using the formula $h = \frac{A}{b}$:
$h = \frac{16.38 \text{ cm}^2}{15.6 \text{ cm}}$
$h = \frac{16.38}{15.6} \text{ cm}$
$h = 1.05 \text{ cm}$
The missing height is 1.05 cm.
Here is the table with the missing values filled in:
| S.No. | Base | Height | Area of the Parallelogram |
| a. | 20 cm | 12.3 cm | 246 cm$^2$ |
| b. | 10.3 cm | 15 cm | 154.5 cm$^2$ |
| c. | 5.8 cm | 8.4 cm | 48.72 cm$^2$ |
| d. | 15.6 cm | 1.05 cm | 16.38 cm$^2$ |
Question 4. Find the missing values:
| Base | Height | Area OF Triangle |
|---|---|---|
| 15 cm | ______ | 87 cm2 |
| ______ | 31.4 mm | 1256 mm2 |
| 22 cm | ______ | 170.5 cm2 |
Answer:
Solution:
The area of a triangle is given by the formula:
$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $
$ A = \frac{1}{2} \times b \times h $
We can find the missing value by rearranging the formula:
If base ($b$) is missing: $b = \frac{2 \times A}{h}$
If height ($h$) is missing: $h = \frac{2 \times A}{b}$
Row 1:
Given: Base ($b$) = 15 cm, Area ($A$) = 87 cm$^2$.
To find: Height ($h$).
Using the formula $h = \frac{2 \times A}{b}$:
$h = \frac{2 \times 87 \text{ cm}^2}{15 \text{ cm}}$
$h = \frac{174}{15} \text{ cm}$
Simplify the fraction by dividing numerator and denominator by 3:
$h = \frac{174 \div 3}{15 \div 3} \text{ cm} = \frac{58}{5} \text{ cm}$.
As a decimal: $h = 11.6 \text{ cm}$.
The missing height is 11.6 cm.
Row 2:
Given: Height ($h$) = 31.4 mm, Area ($A$) = 1256 mm$^2$.
To find: Base ($b$).
Using the formula $b = \frac{2 \times A}{h}$:
$b = \frac{2 \times 1256 \text{ mm}^2}{31.4 \text{ mm}}$
$b = \frac{2512}{31.4} \text{ mm}$.
To perform the division, multiply the numerator and the denominator by 10 to remove the decimal:
$b = \frac{25120}{314} \text{ mm}$.
Perform the division:
$25120 \div 314 = 80$.
$b = 80 \text{ mm}$.
The missing base is 80 mm.
Row 3:
Given: Base ($b$) = 22 cm, Area ($A$) = 170.5 cm$^2$.
To find: Height ($h$).
Using the formula $h = \frac{2 \times A}{b}$:
$h = \frac{2 \times 170.5 \text{ cm}^2}{22 \text{ cm}}$
$h = \frac{341}{22} \text{ cm}$.
Perform the division:
$341 \div 22 = 15.5$.
$h = 15.5 \text{ cm}$.
The missing height is 15.5 cm.
Here is the table with the missing values filled in:
| Base | Height | Area OF Triangle |
| 15 cm | 11.6 cm | 87 cm$^2$ |
| 80 mm | 31.4 mm | 1256 mm$^2$ |
| 22 cm | 15.5 cm | 170.5 cm$^2$ |
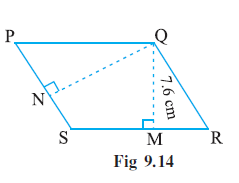
Question 5. PQRS is a parallelogram (Fig 9.14). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
(a) the area of the parallegram PQRS
(b) QN, if PS = 8 cm
Answer:
Given:
PQRS is a parallelogram.
QM is the height from Q to base SR.
QN is the height from Q to base PS.
SR = 12 cm.
QM = 7.6 cm.
PS = 8 cm.
To Find:
(a) The area of the parallelogram PQRS.
(b) The length of QN.
Solution:
(a) The area of the parallelogram PQRS:
The area of a parallelogram is given by the formula:
$ \text{Area} = \text{base} \times \text{corresponding height} $
$ A = b \times h $
We are given the base SR and its corresponding height QM.
Base (SR) = 12 cm.
Corresponding height (QM) = 7.6 cm.
Substitute the values into the formula:
$ \text{Area of Parallelogram PQRS} = \text{SR} \times \text{QM} $
$ \text{Area} = 12 \text{ cm} \times 7.6 \text{ cm} $
$ \text{Area} = (12 \times 7.6) \text{ cm}^2 $
$ \text{Area} = 91.2 \text{ cm}^2 $
The area of the parallelogram PQRS is $91.2 \text{ cm}^2$.
(b) QN, if PS = 8 cm:
We know the area of the parallelogram PQRS from part (a) is $91.2 \text{ cm}^2$.
We can use the same area formula with a different base and its corresponding height.
The base is PS = 8 cm.
The corresponding height is QN (which we need to find).
$ \text{Area of Parallelogram PQRS} = \text{PS} \times \text{QN} $
Substitute the known values:
$91.2 \text{ cm}^2 = 8 \text{ cm} \times \text{QN}$
To find QN, rearrange the equation:
$ \text{QN} = \frac{91.2 \text{ cm}^2}{8 \text{ cm}} $
$ \text{QN} = \frac{91.2}{8} \text{ cm} $
$ \text{QN} = 11.4 \text{ cm} $
The length of QN is 11.4 cm.
Conclusion:
(a) The area of the parallelogram PQRS is $91.2 \text{ cm}^2$.
(b) The length of QN is 11.4 cm.
Question 6. DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (Fig 9.15). If the area of the parallelogram is 1470 cm2 , AB = 35 cm and AD = 49 cm, find the length of BM and DL.

Answer:
Given:
ABCD is a parallelogram.
DL is the height on side AB.
BM is the height on side AD.
Area of parallelogram ABCD = $1470 \text{ cm}^2$.
AB = 35 cm.
AD = 49 cm.
To Find:
The lengths of BM and DL.
Solution:
The area of a parallelogram is given by the formula:
$ \text{Area} = \text{base} \times \text{corresponding height} $
$ A = b \times h $
We can use the given area and side lengths to find the corresponding heights.
To find the length of DL:
DL is the height corresponding to the base AB.
Base (AB) = 35 cm.
Height (DL) = ?
Area = $1470 \text{ cm}^2$.
Using the area formula:
$ \text{Area} = \text{AB} \times \text{DL} $
$1470 \text{ cm}^2 = 35 \text{ cm} \times \text{DL}$
To find DL, rearrange the equation:
$ \text{DL} = \frac{1470 \text{ cm}^2}{35 \text{ cm}} $
$ \text{DL} = \frac{1470}{35} \text{ cm} $
Perform the division:
$1470 \div 35 = 42$.
$ \text{DL} = 42 \text{ cm} $
The length of DL is 42 cm.
To find the length of BM:
BM is the height corresponding to the base AD.
Base (AD) = 49 cm.
Height (BM) = ?
Area = $1470 \text{ cm}^2$.
Using the area formula:
$ \text{Area} = \text{AD} \times \text{BM} $
$1470 \text{ cm}^2 = 49 \text{ cm} \times \text{BM}$
To find BM, rearrange the equation:
$ \text{BM} = \frac{1470 \text{ cm}^2}{49 \text{ cm}} $
$ \text{BM} = \frac{1470}{49} \text{ cm} $
Perform the division:
$1470 \div 49 = 30$.
$ \text{BM} = 30 \text{ cm} $
The length of BM is 30 cm.
Conclusion:
The length of DL is 42 cm.
The length of BM is 30 cm.
Question 7. ∆ABC is right angled at A (Fig 9.16). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ∆ABC. Also find the length of AD.

Answer:
Given:
$\Delta$ABC is right-angled at A.
AD $\perp$ BC.
AB = 5 cm.
BC = 13 cm.
AC = 12 cm.
To Find:
The area of $\Delta$ABC.
The length of AD.
Solution:
Area of $\Delta$ABC:
Since $\Delta$ABC is right-angled at A, we can consider AB as the base and AC as the corresponding height (or vice-versa).
The area of a triangle is given by the formula:
$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $
Using base AB and height AC:
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times \text{AB} \times \text{AC} $
Substitute the given values:
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times 5 \text{ cm} \times 12 \text{ cm} $
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times 60 \text{ cm}^2 $
$ \text{Area of } \Delta \text{ABC} = 30 \text{ cm}^2 $
The area of the triangle ABC is $30 \text{ cm}^2$.
Length of AD:
We know the area of $\Delta$ABC is $30 \text{ cm}^2$.
AD is the height corresponding to the base BC.
Base (BC) = 13 cm.
Height (AD) = ?
Using the area formula with base BC and height AD:
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times \text{BC} \times \text{AD} $
Substitute the known values:
$30 \text{ cm}^2 = \frac{1}{2} \times 13 \text{ cm} \times \text{AD}$
Simplify and rearrange the equation to solve for AD:
$30 = \frac{13}{2} \times \text{AD}$
Multiply both sides by 2:
$30 \times 2 = 13 \times \text{AD}$
$60 = 13 \times \text{AD}$
Divide both sides by 13:
$ \text{AD} = \frac{60}{13} \text{ cm} $
The length of AD is $\frac{60}{13}$ cm.
Conclusion:
The area of $\Delta$ABC is $30 \text{ cm}^2$.
The length of AD is $\frac{60}{13}$ cm.
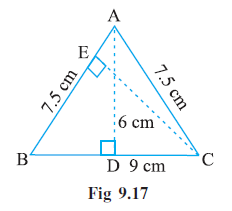
Question 8. ∆ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (Fig 9.17). The height AD from A to BC, is 6 cm. Find the area of ∆ABC. What will be the height from C to AB i.e., CE?
Answer:
Given:
$\Delta$ABC is an isosceles triangle with AB = AC = 7.5 cm.
BC = 9 cm.
AD is the height from A to BC, AD = 6 cm.
CE is the height from C to AB.
To Find:
The area of $\Delta$ABC.
The length of the height CE.
Solution:
Area of $\Delta$ABC:
The area of a triangle is given by the formula:
$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{corresponding height} $
$ A = \frac{1}{2} \times b \times h $
We are given the base BC and its corresponding height AD.
Base (BC) = 9 cm.
Corresponding height (AD) = 6 cm.
Substitute the values into the formula:
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times \text{BC} \times \text{AD} $
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times 9 \text{ cm} \times 6 \text{ cm} $
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times 54 \text{ cm}^2 $
$ \text{Area of } \Delta \text{ABC} = 27 \text{ cm}^2 $
The area of the triangle ABC is $27 \text{ cm}^2$.
The height from C to AB (CE):
We know the area of $\Delta$ABC is $27 \text{ cm}^2$.
CE is the height corresponding to the base AB.
Base (AB) = 7.5 cm.
Height (CE) = ?
Using the area formula with base AB and height CE:
$ \text{Area of } \Delta \text{ABC} = \frac{1}{2} \times \text{AB} \times \text{CE} $
Substitute the known values:
$27 \text{ cm}^2 = \frac{1}{2} \times 7.5 \text{ cm} \times \text{CE}$
Simplify and rearrange the equation to solve for CE:
$27 = \frac{1}{2} \times \frac{75}{10} \times \text{CE}$
$27 = \frac{1}{2} \times \frac{15}{2} \times \text{CE}$
$27 = \frac{15}{4} \times \text{CE}$
Multiply both sides by 4 and divide by 15:
$ \text{CE} = \frac{27 \times 4}{15} \text{ cm} $
$ \text{CE} = \frac{\cancel{27}^{9} \times 4}{\cancel{15}_{5}} \text{ cm} $
$ \text{CE} = \frac{9 \times 4}{5} \text{ cm} $
$ \text{CE} = \frac{36}{5} \text{ cm} $
As a decimal: $ \text{CE} = 7.2 \text{ cm} $. ($36 \div 5 = 7.2$).
The height from C to AB (CE) is $\frac{36}{5}$ cm or 7.2 cm.
Conclusion:
The area of $\Delta$ABC is $27 \text{ cm}^2$.
The height CE is $\frac{36}{5}$ cm (or 7.2 cm).
Example 7 to 14 (Before Exercise 9.2)
Example 7. What is the circumference of a circle of diameter 10cm (Take π = 3.14)?
Answer:
Given:
Diameter of the circle ($d$) = 10 cm.
Value of $\pi$ to be used = 3.14.
To Find:
The circumference of the circle.
Solution:
The circumference of a circle is given by the formula:
$ \text{Circumference} = \pi \times \text{diameter} $
$ C = \pi d $
Substitute the given values into the formula:
$ C = 3.14 \times 10 \text{ cm} $
$ C = 31.4 \text{ cm} $
The unit of circumference is the same as the unit of length, which is cm.
Conclusion: The circumference of the circle is 31.4 cm.
Example 8. What is the circumference of a circular disc of radius 14 cm? $\left(Use \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Radius of the circular disc ($r$) = 14 cm.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The circumference of the circular disc.
Solution:
The circumference of a circle is given by the formula:
$ \text{Circumference} = 2 \times \pi \times \text{radius} $
$ C = 2 \pi r $
Substitute the given values into the formula:
$ C = 2 \times \frac{22}{7} \times 14 \text{ cm} $
Perform the calculation:
$ C = 2 \times \frac{22}{\cancel{7}^{1}} \times \cancel{14}^{2} \text{ cm} $
$ C = 2 \times 22 \times 2 \text{ cm} $
$ C = 4 \times 22 \text{ cm} $
$ C = 88 \text{ cm} $
The unit of circumference is cm.
Conclusion: The circumference of the circular disc is 88 cm.
Example 9. The radius of a circular pipe is 10 cm. What length of a tape is required to wrap once around the pipe (π = 3.14)?
Answer:
Given:
Radius of the circular pipe ($r$) = 10 cm.
Value of $\pi$ to be used = 3.14.
To Find:
The length of tape required to wrap once around the pipe.
Solution:
The length of tape required to wrap once around the circular pipe is equal to the circumference of the pipe.
The circumference of a circle is given by the formula:
$ \text{Circumference} = 2 \times \pi \times \text{radius} $
$ C = 2 \pi r $
Substitute the given values into the formula:
$ C = 2 \times 3.14 \times 10 \text{ cm} $
$ C = 6.28 \times 10 \text{ cm} $
$ C = 62.8 \text{ cm} $
The length of the tape required is equal to the circumference, which is 62.8 cm.
Conclusion: The length of a tape required to wrap once around the pipe is 62.8 cm.
Example 10. Find the perimeter of the given shape (Fig 9.23) $\left(Take \;\pi =\frac{22}{7} \right)$?

Answer:
Given:
The shape is formed by four semicircles attached to the sides of a central figure (which appears to be a square, where the sides are the diameters of the semicircles).
The diameter of each semicircle is 14 cm.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The perimeter of the given shape.
Solution:
The perimeter of the given figure is the length of its outer boundary.
The outer boundary is made up of the curved parts of the four semicircles. The sides of the inner square are not part of the boundary.
The diameter of each semicircle is given as 14 cm.
The circumference of a full circle with diameter $d$ is given by the formula $C = \pi d$.
The circumference of a semicircle is half the circumference of the corresponding full circle.
Circumference of one semicircle = $\frac{1}{2} \times \pi \times \text{diameter}$.
Substitute the given values:
Circumference of one semicircle = $\frac{1}{2} \times \frac{22}{7} \times 14 \text{ cm}$.
Calculate the value:
Circumference of one semicircle = $\frac{1}{\cancel{2}_{1}} \times \frac{22}{\cancel{7}_{1}} \times \cancel{14}^{\cancel2} \text{ cm}$.
Circumference of one semicircle = $22 \times 1 \text{ cm} = 22 \text{ cm}$.
The given figure has 4 such semicircles forming its outer boundary.
Perimeter of the figure = Sum of the circumferences of the 4 semicircles.
Perimeter = $4 \times (\text{Circumference of one semicircle})$.
Perimeter = $4 \times 22 \text{ cm}$.
Calculate the total perimeter:
Perimeter = $88 \text{ cm}$.
Conclusion: The perimeter of the given shape is 88 cm.
Example 11. Sudhanshu divides a circular disc of radius 7 cm in two equal parts. What is the perimeter of each semicircular shape disc? $\left(Use \;\pi =\frac{22}{7} \right)$
Answer:
Given:
A circular disc is divided into two equal semicircular parts.
Radius of the circular disc ($r$) = 7 cm.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The perimeter of each semicircular shape disc.
Solution:
When a circular disc is divided into two equal semicircular parts, each part's boundary consists of a curved edge (the semicircle) and a straight edge (the diameter of the original circle).
The length of the curved edge of a semicircle is half the circumference of the full circle.
The circumference of the full circle with radius $r$ is $2 \pi r$.
Length of the curved edge of the semicircle = $\frac{1}{2} \times 2 \pi r = \pi r$.
Radius ($r$) = 7 cm.
Value of $\pi = \frac{22}{7}$.
Length of the curved edge = $\frac{22}{7} \times 7 \text{ cm}$.
Length of the curved edge = $\frac{22}{\cancel{7}^{1}} \times \cancel{7}^{1} \text{ cm} = 22 \text{ cm}$.
The straight edge of the semicircle is the diameter of the original circle.
Diameter ($d$) = $2 \times \text{radius} = 2 \times 7 \text{ cm} = 14 \text{ cm}$.
The perimeter of each semicircular shape disc is the sum of the length of its curved edge and the length of its straight edge.
Perimeter = (Length of curved edge) + (Length of straight edge)
Perimeter = $22 \text{ cm} + 14 \text{ cm}$
Perimeter = $36 \text{ cm}$.
Conclusion: The perimeter of each semicircular shape disc is 36 cm.
Example 12. Find the area of a circle of radius 30 cm (use π = 3.14).
Answer:
Given:
Radius of the circle ($r$) = 30 cm.
Value of $\pi$ to be used = 3.14.
To Find:
The area of the circle.
Solution:
The area of a circle is given by the formula:
$ \text{Area} = \pi \times (\text{radius})^2 $
$ A = \pi r^2 $
Substitute the given values into the formula:
$ A = 3.14 \times (30 \text{ cm})^2 $
$ A = 3.14 \times (30 \times 30) \text{ cm}^2 $
$ A = 3.14 \times 900 \text{ cm}^2 $
Perform the multiplication:
$3.14 \times 900 = 314 \times 9$ (since $900 = 9 \times 100$, and multiplying by 100 shifts the decimal two places to the right).
So, $3.14 \times 900 = 2826$.
$ A = 2826 \text{ cm}^2 $
The unit of area is square centimetres, denoted as $\text{cm}^2$.
Conclusion: The area of a circle of radius 30 cm is $2826 \text{ cm}^2$.
Example 13. Diameter of a circular garden is 9.8 m. Find its area.
Answer:
Given:
Diameter of the circular garden ($d$) = 9.8 m.
Unless specified, we generally use $\pi = \frac{22}{7}$ when the radius or diameter is a multiple of 7 or can be easily simplified with 7. In this case, the diameter 9.8 is $9.8 = \frac{98}{10} = \frac{49}{5}$, which is related to 7.
Let's use $\pi = \frac{22}{7}$.
To Find:
The area of the circular garden.
Solution:
The area of a circle is given by the formula $A = \pi r^2$, where $r$ is the radius.
The radius is half of the diameter: $r = \frac{d}{2}$.
$r = \frac{9.8 \text{ m}}{2} = 4.9 \text{ m}$.
Now, substitute the values of $\pi$ and $r$ into the area formula:
$ A = \pi r^2 $
$ A = \frac{22}{7} \times (4.9 \text{ m})^2 $
$ A = \frac{22}{7} \times (4.9 \times 4.9) \text{ m}^2 $
$ A = \frac{22}{7} \times (4.9 \times \frac{49}{10}) \text{ m}^2 $
$ A = 22 \times \frac{4.9}{7} \times 4.9 \text{ m}^2 $
Since $4.9 \div 7 = 0.7$, we have:
$ A = 22 \times 0.7 \times 4.9 \text{ m}^2 $
$ A = 15.4 \times 4.9 \text{ m}^2 $
Perform the multiplication $15.4 \times 4.9$:
$15.4 \times 4.9$ is equivalent to $154 \times 49$ divided by 100.
So, $15.4 \times 4.9 = 75.46$.
$ A = 75.46 \text{ m}^2 $
The unit of area is square metres, denoted as $\text{m}^2$.
Conclusion: The area of the circular garden is $75.46 \text{ m}^2$.
Example 14. The adjoining figure shows two circles with the same centre. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.
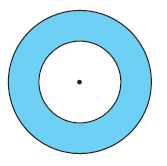
Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. ($\pi$ = 3.14)
Answer:
Given:
Two concentric circles.
Radius of the larger circle ($R$) = 10 cm.
Radius of the smaller circle ($r$) = 4 cm.
Value of $\pi$ to be used = 3.14.
To Find:
(a) The area of the larger circle.
(b) The area of the smaller circle.
(c) The shaded area between the two circles.
Solution:
The area of a circle is given by the formula $A = \pi \times (\text{radius})^2 = \pi r^2$.
(a) The area of the larger circle:
Radius of the larger circle ($R$) = 10 cm.
Area of the larger circle ($A_{large}$) = $\pi R^2$
$A_{large} = 3.14 \times (10 \text{ cm})^2$
$A_{large} = 3.14 \times 100 \text{ cm}^2$
$A_{large} = 314 \text{ cm}^2$
The area of the larger circle is $314 \text{ cm}^2$.
(b) The area of the smaller circle:
Radius of the smaller circle ($r$) = 4 cm.
Area of the smaller circle ($A_{small}$) = $\pi r^2$
$A_{small} = 3.14 \times (4 \text{ cm})^2$
$A_{small} = 3.14 \times 16 \text{ cm}^2$
Perform the multiplication $3.14 \times 16$:
$3.14 \times 16$ is equivalent to $314 \times 16$ divided by 100.
So, $3.14 \times 16 = 50.24$.
$A_{small} = 50.24 \text{ cm}^2$
The area of the smaller circle is $50.24 \text{ cm}^2$.
(c) The shaded area between the two circles:
The shaded area is the region between the larger circle and the smaller circle. Its area is the difference between the area of the larger circle and the area of the smaller circle.
Shaded Area = Area of larger circle - Area of smaller circle
Shaded Area = $A_{large} - A_{small}$
Shaded Area = $314 \text{ cm}^2 - 50.24 \text{ cm}^2$
Shaded Area = $263.76 \text{ cm}^2$.
The shaded area between the two circles is $263.76 \text{ cm}^2$.
Conclusion:
(a) The area of the larger circle is $314 \text{ cm}^2$.
(b) The area of the smaller circle is $50.24 \text{ cm}^2$.
(c) The shaded area between the two circles is $263.76 \text{ cm}^2$.
Exercise 9.3
Question 1. Find the circumference of the circles with the following radius: $\left(Take \;\pi =\frac{22}{7} \right)$
(a) 14 cm
(b) 28 mm
(c) 21 cm
Answer:
Solution:
The circumference of a circle with radius $r$ is given by the formula:
$ \text{Circumference} = 2 \pi r $
We are asked to use $\pi = \frac{22}{7}$.
(a) Radius = 14 cm
Substitute $r = 14$ cm and $\pi = \frac{22}{7}$ into the formula:
$ C = 2 \times \frac{22}{7} \times 14 \text{ cm} $
$ C = 2 \times \frac{22}{\cancel{7}^{1}} \times \cancel{14}^{2} \text{ cm} $
$ C = 2 \times 22 \times 2 \text{ cm} $
$ C = 4 \times 22 \text{ cm} $
$ C = 88 \text{ cm} $
The circumference of the circle is 88 cm.
(b) Radius = 28 mm
Substitute $r = 28$ mm and $\pi = \frac{22}{7}$ into the formula:
$ C = 2 \times \frac{22}{7} \times 28 \text{ mm} $
$ C = 2 \times \frac{22}{\cancel{7}^{1}} \times \cancel{28}^{4} \text{ mm} $
$ C = 2 \times 22 \times 4 \text{ mm} $
$ C = 8 \times 22 \text{ mm} $
$ C = 176 \text{ mm} $
The circumference of the circle is 176 mm.
(c) Radius = 21 cm
Substitute $r = 21$ cm and $\pi = \frac{22}{7}$ into the formula:
$ C = 2 \times \frac{22}{7} \times 21 \text{ cm} $
$ C = 2 \times \frac{22}{\cancel{7}^{1}} \times \cancel{21}^{3} \text{ cm} $
$ C = 2 \times 22 \times 3 \text{ cm} $
$ C = 6 \times 22 \text{ cm} $
$ C = 132 \text{ cm} $
The circumference of the circle is 132 cm.
Question 2. Find the area of the following circles, given that:
(a) radius = 14 mm $\left(Take \;\pi =\frac{22}{7} \right)$
(b) diameter = 49 m
(c) radius = 5 cm
Answer:
The area of a circle with radius $r$ is given by the formula:
$ A = \pi r^2 $
(a) radius = 14 mm
Given: Radius ($r$) = 14 mm, $\pi = \frac{22}{7}$.
To Find: Area of the circle.
Using the formula $A = \pi r^2$:
$ A = \frac{22}{7} \times (14 \text{ mm})^2 $
$ A = \frac{22}{7} \times 14 \text{ mm} \times 14 \text{ mm} $
$ A = \frac{22}{\cancel{7}^{1}} \times \cancel{14}^{2} \times 14 \text{ mm}^2 $
$ A = 22 \times 2 \times 14 \text{ mm}^2 $
$ A = 44 \times 14 \text{ mm}^2 $
$ A = 616 \text{ mm}^2 $
The area of the circle is $616 \text{ mm}^2$.
(b) diameter = 49 m
Given: Diameter ($d$) = 49 m. We will use $\pi = \frac{22}{7}$ since the diameter is a multiple of 7.
To Find: Area of the circle.
First, find the radius from the diameter: $r = \frac{d}{2}$.
$ r = \frac{49}{2} \text{ m} $
Using the formula $A = \pi r^2$:
$ A = \frac{22}{7} \times \left(\frac{49}{2} \text{ m}\right)^2 $
$ A = \frac{22}{7} \times \frac{49}{2} \text{ m} \times \frac{49}{2} \text{ m} $
$ A = \frac{\cancel{22}^{11}}{\cancel{7}^{1}} \times \frac{\cancel{49}^{7}}{2} \times \frac{49}{\cancel{2}^{1}} \text{ m}^2 $
$ A = 11 \times 7 \times \frac{49}{2} \text{ m}^2 $
$ A = 77 \times \frac{49}{2} \text{ m}^2 $
$ A = \frac{77 \times 49}{2} \text{ m}^2 $
$ A = \frac{3773}{2} \text{ m}^2 $
As a decimal: $A = 1886.5 \text{ m}^2$.
The area of the circle is $\frac{3773}{2}$ m$^2$ or 1886.5 m$^2$.
(c) radius = 5 cm
Given: Radius ($r$) = 5 cm. We will use $\pi = 3.14$ as typically done when a multiple of 7 is not involved, unless specified otherwise.
To Find: Area of the circle.
Using the formula $A = \pi r^2$:
$ A = 3.14 \times (5 \text{ cm})^2 $
$ A = 3.14 \times (5 \times 5) \text{ cm}^2 $
$ A = 3.14 \times 25 \text{ cm}^2 $
$ A = 78.5 \text{ cm}^2 $
The area of the circle is $78.5 \text{ cm}^2$.
Question 3. If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. $\left(Take \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Circumference of the circular sheet ($C$) = 154 m.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The radius of the sheet ($r$).
The area of the sheet ($A$).
Solution:
The circumference of a circle is given by the formula $C = 2 \pi r$.
Substitute the given values into the circumference formula to find the radius:
$154 \text{ m} = 2 \times \frac{22}{7} \times r$
Simplify the right side:
$154 = \frac{44}{7} \times r$
To find $r$, multiply both sides by $\frac{7}{44}$:
$ r = 154 \times \frac{7}{44} $
$ r = \frac{154 \times 7}{44} $
Cancel out common factors. Both 154 and 44 are divisible by 2 and 11.
Divide both by 2: $\frac{\cancel{154}^{77} \times 7}{\cancel{44}_{22}}$
Divide both by 11: $\frac{\cancel{77}^{7} \times 7}{\cancel{22}_{2}}$
$ r = \frac{7 \times 7}{2} = \frac{49}{2} $
$ r = 24.5 \text{ m} $
The radius of the circular sheet is $\frac{49}{2}$ m or 24.5 m.
Now, find the area of the circular sheet using the formula $A = \pi r^2$ and the calculated radius.
$ A = \frac{22}{7} \times \left(\frac{49}{2} \text{ m}\right)^2 $
$ A = \frac{22}{7} \times \frac{49}{2} \text{ m} \times \frac{49}{2} \text{ m} $
$ A = \frac{\cancel{22}^{11}}{\cancel{7}^{1}} \times \frac{\cancel{49}^{7}}{2} \times \frac{49}{\cancel{2}^{1}} \text{ m}^2 $
$ A = 11 \times 7 \times \frac{49}{2} \text{ m}^2 $
$ A = 77 \times \frac{49}{2} \text{ m}^2 $
$ A = \frac{77 \times 49}{2} \text{ m}^2 $
$ A = \frac{3773}{2} \text{ m}^2 $
As a decimal: $ A = 1886.5 \text{ m}^2 $. ($3773 \div 2 = 1886.5$).
The area of the circular sheet is $\frac{3773}{2}$ m$^2$ or 1886.5 m$^2$.
Conclusion:
The radius of the circular sheet is 24.5 m.
The area of the circular sheet is 1886.5 m$^2$.
Question 4. A gardener wants to fence a circular garden of diameter 21m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs ₹ 4 per meter. $\left(Take \;\pi =\frac{22}{7} \right)$

Answer:
Given:
Diameter of the circular garden ($d$) = 21 m.
Number of rounds of fence = 2.
Cost of rope per meter = $\textsf{₹}$ 4.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The total length of rope needed.
The total cost of the rope.
Solution:
The length of rope needed for one round of fence is equal to the circumference of the circular garden.
The circumference of a circle is given by the formula $C = \pi d$, where $d$ is the diameter.
Calculate the circumference for one round:
$ C = \pi d $
$ C = \frac{22}{7} \times 21 \text{ m} $
$ C = \frac{22}{\cancel{7}^{1}} \times \cancel{21}^{3} \text{ m} $
$ C = 22 \times 3 \text{ m} $
$ C = 66 \text{ m} $
The length of rope needed for one round is 66 m.
The gardener makes 2 rounds of fence. The total length of rope needed is the circumference multiplied by the number of rounds.
Total length of rope = Circumference for one round $\times$ Number of rounds
Total length of rope = $66 \text{ m} \times 2$
Total length of rope = $132 \text{ m}$.
The total length of rope the gardener needs to purchase is 132 m.
Now, calculate the cost of the rope.
Cost of rope per meter = $\textsf{₹}$ 4.
Total cost = Total length of rope $\times$ Cost per meter
Total cost = $132 \text{ m} \times \textsf{₹}\ 4/\text{m}$
Total cost = $\textsf{₹}\ (132 \times 4)$
Total cost = $\textsf{₹}\ 528$.
The total cost of the rope is $\textsf{₹}\ 528$.
Conclusion:
The length of rope needed is 132 m.
The cost of the rope is $\textsf{₹}\ 528$.
Question 5. From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Answer:
Given:
Radius of the large circular sheet ($R$) = 4 cm.
Radius of the smaller circle removed ($r$) = 3 cm.
Value of $\pi$ to be used = 3.14.
To Find:
The area of the remaining sheet.
Solution:
The area of the remaining sheet is the area of the larger circle minus the area of the smaller circle that is removed.
The area of a circle is given by the formula $A = \pi r^2$.
Area of the large circular sheet ($A_{large}$):
$A_{large} = \pi R^2$
$A_{large} = 3.14 \times (4 \text{ cm})^2$
$A_{large} = 3.14 \times 16 \text{ cm}^2$
$A_{large} = 50.24 \text{ cm}^2$.
Area of the smaller circle removed ($A_{small}$):
$A_{small} = \pi r^2$
$A_{small} = 3.14 \times (3 \text{ cm})^2$
$A_{small} = 3.14 \times 9 \text{ cm}^2$
$A_{small} = 28.26 \text{ cm}^2$.
Area of the remaining sheet = $A_{large} - A_{small}$.
Area of remaining sheet = $50.24 \text{ cm}^2 - 28.26 \text{ cm}^2$.
Area of remaining sheet = $21.98 \text{ cm}^2$.
Conclusion: The area of the remaining sheet is $21.98 \text{ cm}^2$.
Question 6. Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs ₹ 15. (Take π = 3.14)
Answer:
Given:
Diameter of the circular table cover ($d$) = 1.5 m.
Cost of lace per meter = $\textsf{₹}$ 15.
Value of $\pi$ to be used = 3.14.
To Find:
The length of lace required.
The cost of the lace.
Solution:
The length of the lace required to put on the edge of the circular table cover is equal to the circumference of the table cover.
The circumference of a circle is given by the formula $C = \pi d$, where $d$ is the diameter.
Calculate the circumference:
$ C = \pi d $
$ C = 3.14 \times 1.5 \text{ m} $
$ C = 4.71 \text{ m} $
The length of lace required is 4.71 m.
Now, calculate the cost of the lace.
Cost of lace per meter = $\textsf{₹}$ 15.
Total cost = Length of lace required $\times$ Cost per meter
Total cost = $4.71 \text{ m} \times \textsf{₹}\ 15/\text{m}$
Total cost = $\textsf{₹}\ (4.71 \times 15)$
Total cost = $\textsf{₹}\ 70.65$.
Conclusion:
The length of lace required is 4.71 m.
The cost of the lace is $\textsf{₹}\ 70.65$.
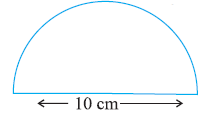
Question 7. Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
Answer:
Given:
The figure is a semicircle including its diameter.
The diameter shown in the figure is 10 cm.
Unless specified, we will use $\pi = \frac{22}{7}$ or $\pi = 3.14$. Given the diameter is 10 cm, using $\pi = 3.14$ might be more convenient for decimal calculations. Let's use $\pi = 3.14$ for this example.
To Find:
The perimeter of the figure.
Solution:
The perimeter of the shape is the total length of its boundary. The boundary consists of the curved part (semicircle) and the straight part (diameter).
The diameter of the semicircle ($d$) = 10 cm.
The radius of the semicircle ($r$) = $\frac{d}{2} = \frac{10}{2} = 5 \text{ cm}$.
The length of the curved part is half the circumference of the full circle with the same diameter.
The circumference of a full circle with diameter $d$ is $C = \pi d$.
Length of the curved part (semicircle) = $\frac{1}{2} \times \pi d$.
Using $\pi = 3.14$ and $d = 10$ cm:
Length of the curved part = $\frac{1}{2} \times 3.14 \times 10 \text{ cm}$
Length of the curved part = $\frac{1}{2} \times 31.4 \text{ cm}$
Length of the curved part = $15.7 \text{ cm}$.
The straight part of the boundary is the diameter, which is 10 cm.
The perimeter of the shape is the sum of the length of the curved part and the length of the straight part.
Perimeter = (Length of semicircle) + (Length of diameter)
Perimeter = $15.7 \text{ cm} + 10 \text{ cm}$
Perimeter = $25.7 \text{ cm}$.
Conclusion: The perimeter of the given figure is 25.7 cm.
Question 8. Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2 . (Take π = 3.14)
Answer:
Given:
Diameter of the circular table-top ($d$) = 1.6 m.
Rate of polishing = $\textsf{₹}$ 15 per m$^2$.
Value of $\pi$ to be used = 3.14.
To Find:
The cost of polishing the circular table-top.
Solution:
The cost of polishing depends on the area of the table-top and the rate of polishing per unit area.
First, find the area of the circular table-top using the formula $A = \pi r^2$, where $r$ is the radius.
The radius is half of the diameter: $r = \frac{d}{2}$.
$r = \frac{1.6 \text{ m}}{2} = 0.8 \text{ m}$.
Now, calculate the area using the formula $A = \pi r^2$:
$ A = 3.14 \times (0.8 \text{ m})^2 $
$ A = 3.14 \times (0.8 \times 0.8) \text{ m}^2 $
$ A = 3.14 \times 0.64 \text{ m}^2 $
$ A = 2.0096 \text{ m}^2 $
The area of the circular table-top is $2.0096 \text{ m}^2$.
Now, calculate the cost of polishing.
Cost = Area $\times$ Rate per unit area
Cost = $2.0096 \text{ m}^2 \times \textsf{₹}\ 15/\text{m}^2$
Cost = $\textsf{₹}\ (2.0096 \times 15)$
Cost $\approx \textsf{₹}\ 30.14$.
The cost of polishing the circular table-top is approximately $\textsf{₹}\ 30.14$.
Conclusion: The cost of polishing the circular table-top is $\textsf{₹}\ 30.14$.
Question 9. Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? $\left(Take \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Length of the wire = 44 cm.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
Radius of the circle formed by the wire.
Area of the circle.
Length of each side of the square formed by the wire.
Which figure (circle or square) encloses more area.
Solution:
When the wire is bent into the shape of a circle, the length of the wire becomes the circumference of the circle.
Circumference of the circle ($C$) = Length of the wire = 44 cm.
The formula for the circumference of a circle is $C = 2 \pi r$, where $r$ is the radius.
Using the formula to find the radius:
$44 \text{ cm} = 2 \times \frac{22}{7} \times r$
Simplify the right side:
$44 = \frac{44}{7} \times r$
To find $r$, multiply both sides by $\frac{7}{44}$:
$ r = 44 \times \frac{7}{44} $
$ r = \frac{\cancel{44}^{1} \times 7}{\cancel{44}_{1}} $
$ r = 7 \text{ cm} $
The radius of the circle is 7 cm.
Now, find the area of the circle using the formula $A_{circle} = \pi r^2$:
$ A_{circle} = \frac{22}{7} \times (7 \text{ cm})^2 $
$ A_{circle} = \frac{22}{7} \times 7 \text{ cm} \times 7 \text{ cm} $
$ A_{circle} = \frac{22}{\cancel{7}^{1}} \times \cancel{7}^{1} \times 7 \text{ cm}^2 $
$ A_{circle} = 22 \times 7 \text{ cm}^2 $
$ A_{circle} = 154 \text{ cm}^2 $
The area of the circle is $154 \text{ cm}^2$.
If the same wire is bent into the shape of a square, the length of the wire becomes the perimeter of the square.
Perimeter of the square = Length of the wire = 44 cm.
The perimeter of a square is given by the formula $P = 4 \times \text{side}$, where 'side' is the length of each side.
Using the formula to find the length of each side:
$ 44 \text{ cm} = 4 \times \text{side} $
Divide both sides by 4:
$ \text{side} = \frac{44}{4} \text{ cm} $
$ \text{side} = 11 \text{ cm} $
The length of each side of the square is 11 cm.
Now, find the area of the square using the formula $A_{square} = \text{side} \times \text{side} = (\text{side})^2$:
$ A_{square} = (11 \text{ cm})^2 $
$ A_{square} = 11 \text{ cm} \times 11 \text{ cm} $
$ A_{square} = 121 \text{ cm}^2 $
The area of the square is $121 \text{ cm}^2$.
Compare the areas of the circle and the square:
Area of the circle = $154 \text{ cm}^2$.
Area of the square = $121 \text{ cm}^2$.
Since $154 > 121$, the area of the circle is greater than the area of the square.
Conclusion:
The radius of the circle is 7 cm.
The area of the circle is $154 \text{ cm}^2$.
The length of each side of the square is 11 cm.
The circle encloses more area than the square.
Question 10. From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1cm are removed. (as shown in the adjoining figure). Find the area of the remaining sheet. $\left(Take \;\pi =\frac{22}{7} \right)$

Answer:
Given:
Radius of the large circular card sheet ($R$) = 14 cm.
Two smaller circles are removed, each with radius ($r_1$) = 3.5 cm.
A rectangle is removed with length ($l$) = 3 cm and breadth ($b$) = 1 cm.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The area of the remaining sheet.
Solution:
The area of the remaining sheet is the area of the large circular sheet minus the sum of the areas of the two smaller circles and the area of the rectangle.
Area of the large circular sheet ($A_{large}$):
Using the formula $A = \pi R^2$:
$A_{large} = \frac{22}{7} \times (14 \text{ cm})^2$
$A_{large} = \frac{22}{7} \times 14 \text{ cm} \times 14 \text{ cm} $
$A_{large} = \frac{22}{\cancel{7}^{1}} \times \cancel{14}^{2} \times 14 \text{ cm}^2 $
$A_{large} = 22 \times 2 \times 14 \text{ cm}^2 $
$A_{large} = 44 \times 14 \text{ cm}^2 $
$A_{large} = 616 \text{ cm}^2$.
Area of one smaller circle ($A_{small\_circle}$):
Radius ($r_1$) = 3.5 cm $= \frac{35}{10} \text{ cm} = \frac{7}{2} \text{ cm}$.
Using the formula $A = \pi r_1^2$:
$A_{small\_circle} = \frac{22}{7} \times \left(\frac{7}{2} \text{ cm}\right)^2 $
$A_{small\_circle} = \frac{22}{7} \times \frac{7}{2} \text{ cm} \times \frac{7}{2} \text{ cm} $
$A_{small\_circle} = \frac{\cancel{22}^{11}}{\cancel{7}^{1}} \times \frac{\cancel{7}^{1}}{\cancel{2}^{1}} \times \frac{7}{2} \text{ cm}^2 $
$A_{small\_circle} = 11 \times 1 \times \frac{7}{2} \text{ cm}^2 = \frac{77}{2} \text{ cm}^2$.
$A_{small\_circle} = 38.5 \text{ cm}^2$.
Area of two smaller circles ($A_{two\_circles}$):
$A_{two\_circles} = 2 \times A_{small\_circle}$
$A_{two\_circles} = 2 \times \frac{77}{2} \text{ cm}^2 = 77 \text{ cm}^2$.
Or, $A_{two\_circles} = 2 \times 38.5 \text{ cm}^2 = 77 \text{ cm}^2$.
Area of the rectangle ($A_{rectangle}$):
Using the formula $A = \text{length} \times \text{breadth}$:
$A_{rectangle} = l \times b$
$A_{rectangle} = 3 \text{ cm} \times 1 \text{ cm} $
$A_{rectangle} = 3 \text{ cm}^2 $
Area of the remaining sheet:
Area of remaining sheet = $A_{large} - (A_{two\_circles} + A_{rectangle})$
Area of remaining sheet = $616 \text{ cm}^2 - (77 \text{ cm}^2 + 3 \text{ cm}^2)$
Area of remaining sheet = $616 \text{ cm}^2 - 80 \text{ cm}^2$
Area of remaining sheet = $536 \text{ cm}^2$.
Conclusion: The area of the remaining sheet is $536 \text{ cm}^2$.
Question 11. A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Answer:
Given:
A square piece of aluminium sheet with side length ($s$) = 6 cm.
A circle is cut out from the square with radius ($r$) = 2 cm.
Value of $\pi$ to be used = 3.14.
To Find:
The area of the left over aluminium sheet.
Solution:
The area of the left over aluminium sheet is the area of the square piece minus the area of the circle that is cut out.
Area of the square sheet ($A_{square}$):
The area of a square is given by the formula $A = \text{side} \times \text{side} = s^2$.
$A_{square} = (6 \text{ cm})^2$
$A_{square} = 6 \text{ cm} \times 6 \text{ cm}$
$A_{square} = 36 \text{ cm}^2$.
Area of the circle cut out ($A_{circle}$):
The area of a circle is given by the formula $A = \pi r^2$.
$A_{circle} = 3.14 \times (2 \text{ cm})^2$
$A_{circle} = 3.14 \times (2 \times 2) \text{ cm}^2$
$A_{circle} = 3.14 \times 4 \text{ cm}^2$
$A_{circle} = 12.56 \text{ cm}^2$.
Area of the left over aluminium sheet:
Area of left over sheet = $A_{square} - A_{circle}$.
Area of left over sheet = $36 \text{ cm}^2 - 12.56 \text{ cm}^2$.
Area of left over sheet = $23.44 \text{ cm}^2$.
Conclusion: The area of the left over aluminium sheet is $23.44 \text{ cm}^2$.
Question 12. The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
Answer:
Given:
Circumference of the circle ($C$) = 31.4 cm.
Value of $\pi$ to be used = 3.14.
To Find:
The radius of the circle ($r$).
The area of the circle ($A$).
Solution:
The circumference of a circle is given by the formula $C = 2 \pi r$, where $r$ is the radius.
Substitute the given values into the circumference formula to find the radius:
$31.4 \text{ cm} = 2 \times 3.14 \times r$
Simplify the right side:
$31.4 = 6.28 \times r$
To find $r$, divide the circumference by $2\pi$:
$ r = \frac{31.4 \text{ cm}}{6.28} $
$ r = \frac{31.4}{6.28} \text{ cm} $
To perform the division, multiply the numerator and the denominator by 100 to remove the decimals:
$ r = \frac{31.4 \times 100}{6.28 \times 100} \text{ cm} = \frac{3140}{628} \text{ cm} $
Perform the division:
$3140 \div 628 = 5$. (Since $628 \times 5 = (600+28) \times 5 = 3000 + 140 = 3140$).
$ r = 5 \text{ cm} $
The radius of the circle is 5 cm.
Now, find the area of the circle using the formula $A = \pi r^2$ and the calculated radius.
$ A = 3.14 \times (5 \text{ cm})^2 $
$ A = 3.14 \times (5 \times 5) \text{ cm}^2 $
$ A = 3.14 \times 25 \text{ cm}^2 $
$ A = 78.5 \text{ cm}^2 $
The area of the circle is $78.5 \text{ cm}^2$.
Conclusion:
The radius of the circle is 5 cm.
The area of the circle is $78.5 \text{ cm}^2$.
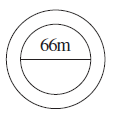
Question 13. A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
Answer:
Given:
Diameter of the circular flower bed ($d_{bed}$) = 66 m.
Width of the path around the flower bed = 4 m.
Value of $\pi$ to be used = 3.14.
To Find:
The area of the path.
Solution:
The path surrounds the flower bed, forming a larger circle with the same center. The area of the path is the area of the larger circle (flower bed + path) minus the area of the smaller circle (flower bed).
First, find the radius of the flower bed ($r_{bed}$):
$r_{bed} = \frac{d_{bed}}{2} = \frac{66 \text{ m}}{2} = 33 \text{ m}$.
The width of the path is added to the radius of the flower bed to get the radius of the larger circle ($R_{total}$).
$R_{total} = r_{bed} + \text{width of path}$
$R_{total} = 33 \text{ m} + 4 \text{ m} = 37 \text{ m}$.
Now, calculate the area of the flower bed ($A_{bed}$):
$A_{bed} = \pi (r_{bed})^2$
$A_{bed} = 3.14 \times (33 \text{ m})^2$
$A_{bed} = 3.14 \times (33 \times 33) \text{ m}^2$
$A_{bed} = 3.14 \times 1089 \text{ m}^2$.
$A_{bed} = 3419.36 \text{ m}^2$.
Calculate the area of the larger circle (flower bed + path) ($A_{total}$):
$A_{total} = \pi (R_{total})^2$
$A_{total} = 3.14 \times (37 \text{ m})^2$
$A_{total} = 3.14 \times (37 \times 37) \text{ m}^2$
$A_{total} = 3.14 \times 1369 \text{ m}^2$.
$A_{total} = 4298.66 \text{ m}^2$.
Area of the path = $A_{total} - A_{bed}$.
Area of the path = $4298.66 \text{ m}^2 - 3419.36 \text{ m}^2$.
Area of the path = $879.30 \text{ m}^2$.
Conclusion: The area of the path is $879.30 \text{ m}^2$.
Question 14. A circular flower garden has an area of 314 m2 . A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
Answer:
Given:
Area of the circular flower garden ($A_{garden}$) = $314 \text{ m}^2$.
Radius of the area the sprinkler can cover ($r_{sprinkler}$) = 12 m.
Value of $\pi$ to be used = 3.14.
To Determine:
Whether the sprinkler can water the entire garden.
Solution:
To determine if the sprinkler can water the entire garden, we need to compare the area covered by the sprinkler with the area of the garden. If the area covered by the sprinkler is greater than or equal to the area of the garden, then it can water the entire garden.
First, calculate the area covered by the sprinkler using the formula $A = \pi r^2$, where $r$ is the radius of the covered area.
Radius of the covered area ($r_{sprinkler}$) = 12 m.
Area covered by sprinkler ($A_{sprinkler}$) = $\pi (r_{sprinkler})^2$
$A_{sprinkler} = 3.14 \times (12 \text{ m})^2$
$A_{sprinkler} = 3.14 \times (12 \times 12) \text{ m}^2$
$A_{sprinkler} = 3.14 \times 144 \text{ m}^2$
$A_{sprinkler} = 452.16 \text{ m}^2$.
Compare the area covered by the sprinkler with the area of the garden:
Area covered by sprinkler = $452.16 \text{ m}^2$.
Area of the garden = $314 \text{ m}^2$.
Since $452.16 \text{ m}^2 > 314 \text{ m}^2$, the area covered by the sprinkler is greater than the area of the garden.
Therefore, the sprinkler can water the entire garden.
Conclusion: Yes, the sprinkler will water the entire garden.
Question 15. Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
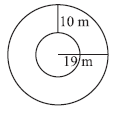
Answer:
Given:
Two concentric circles.
Radius of the outer circle ($R$) = 19 m.
Width of the region between the circles = 10 m.
Value of $\pi$ to be used = 3.14.
To Find:
The circumference of the inner circle.
The circumference of the outer circle.
Solution:
The circumference of a circle with radius $r$ is given by the formula:
$ \text{Circumference} = 2 \pi r $
First, determine the radius of the inner circle ($r$).
The radius of the outer circle ($R$) is the sum of the radius of the inner circle ($r$) and the width of the region between them (10 m).
$ R = r + 10 \text{ m} $
$ 19 \text{ m} = r + 10 \text{ m} $
To find $r$, subtract the width from the outer radius:
$ r = 19 \text{ m} - 10 \text{ m} $
$ r = 9 \text{ m} $
Now, calculate the circumference of the inner circle:
$ C_{inner} = 2 \pi r $
$ C_{inner} = 2 \times 3.14 \times 9 \text{ m} $
$ C_{inner} = 6.28 \times 9 \text{ m} $
$ C_{inner} = 56.52 \text{ m} $
The circumference of the inner circle is 56.52 m.
Next, calculate the circumference of the outer circle:
$ C_{outer} = 2 \pi R $
$ C_{outer} = 2 \times 3.14 \times 19 \text{ m} $
$ C_{outer} = 6.28 \times 19 \text{ m} $
$ C_{outer} = 119.32 \text{ m} $
The circumference of the outer circle is 119.32 m.
Conclusion:
The circumference of the inner circle is 56.52 m.
The circumference of the outer circle is 119.32 m.
Question 16. How many times a wheel of radius 28 cm must rotate to go 352 m? $\left(Take \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Radius of the wheel ($r$) = 28 cm.
Total distance to be covered = 352 m.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The number of times the wheel must rotate.
Solution:
The distance covered by the wheel in one full rotation is equal to its circumference.
First, calculate the circumference of the wheel using the formula $C = 2 \pi r$.
Radius ($r$) = 28 cm.
$ C = 2 \times \frac{22}{7} \times 28 \text{ cm} $
$ C = 2 \times \frac{22}{\cancel{7}^{1}} \times \cancel{28}^{4} \text{ cm} $
$ C = 2 \times 22 \times 4 \text{ cm} $
$ C = 8 \times 22 \text{ cm} $
$ C = 176 \text{ cm} $
The distance covered in one rotation is 176 cm.
The total distance to be covered is given in meters (352 m), while the circumference is in centimeters (176 cm).
We need to convert the total distance to centimeters so that the units are consistent.
1 meter = 100 centimeters.
Total distance in cm = $352 \text{ m} \times 100 \text{ cm/m} = 35200 \text{ cm}$.
The number of rotations is given by the total distance divided by the distance covered in one rotation (circumference).
$ \text{Number of rotations} = \frac{\text{Total distance}}{\text{Circumference}} $
$ \text{Number of rotations} = \frac{35200 \text{ cm}}{176 \text{ cm}} $
Perform the division:
$35200 \div 176$.
We can see that $176 \times 2 = 352$.
So, $35200 \div 176 = (352 \times 100) \div 176 = (176 \times 2 \times 100) \div 176 = 2 \times 100 = 200$.
$ \text{Number of rotations} = 200 $
Conclusion: The wheel must rotate 200 times to go 352 m.
Question 17. The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour. (Take π = 3.14)
Answer:
Given:
Length of the minute hand = 15 cm.
Time duration = 1 hour.
Value of $\pi$ to be used = 3.14.
To Find:
The distance moved by the tip of the minute hand in 1 hour.
Solution:
The tip of the minute hand traces a circular path as it moves around the clock face. The length of the minute hand is the radius of this circular path.
Radius of the circular path ($r$) = Length of the minute hand = 15 cm.
In 1 hour, the minute hand completes one full rotation around the clock face.
The distance moved by the tip of the minute hand in one full rotation is equal to the circumference of the circle it traces.
The circumference of a circle is given by the formula $C = 2 \pi r$, where $r$ is the radius.
Calculate the circumference:
$ C = 2 \times \pi \times r $
$ C = 2 \times 3.14 \times 15 \text{ cm} $
$ C = 6.28 \times 15 \text{ cm} $
$ C = 94.2 \text{ cm} $
The distance the tip of the minute hand moves in 1 hour is equal to the circumference of the circle it traces, which is 94.2 cm.
Conclusion: The tip of the minute hand moves 94.2 cm in 1 hour.

